¿Qué es una función?
La relación entre valores de 2 conjuntos, donde a cada valor de un conjunto le corresponde únicamente 1 valor del otro conjunto.
De manera convencional , nombramos "x" al primer conjunto y "y" al segundo conjunto
x : 0, 1, 2, 3...
y : 0, 1, 2, 3...
La manera de relacionar los valores de cada conjunto se escribe en forma de coordenada , ya que podemos graficarla en un plano.
Los valores del conjunto "x" se escriben a la izquierda de la "," y los valores del conjunto "y" a la derecha.
Puntos en el plano:
(x,y)
(0,0)
(1,1)
(2,2)
(3,3)
La variable "x" toma valores infinitos y la variable "y" depende de estos valores.
A la variable "x" se le llama variable independiente , tú eliges el valor. Mientras que la variable "y" depende de este valor según sea la función.
Ejemplo:
Función cuadrática
y = x2 + 2x + 5
Esta función la podemos definir como una fórmula. Con ella podemos graficar infinitos puntos , que siguen la trayectoria de una parábola , ya que es una función cuadrática (el exponente mayor de la x es 2).
Para obtener cada punto , elegimos distintos valores de "x" y sustituimos en la función para calcular el valor de "y" que depende de "x":
Si x = 1
y = 12 + 2(1) + 5 = 1 + 2 + 5 = 8
Por lo tanto , la coordenada es (1,8)
Si x = 2
y = 22 + 2(2) + 5 = 4 + 4 + 5 = 13
La coordenada es (2,13)
Si x = 0
y = 02 + 2(0) + 5 = 5
La coordenada es (0,5)
Para obtener muchos más puntos, continuamos con este procedimiento y al graficarlos en la app Desmos, obtenemos esta parábola:
Ejemplos de funciones y sus gráficas
Existen muchos tipos de funciones y todas son gráficas distintas.
Funciones cúbicas
El mayor exponente de la variable independiente "x" es 3.
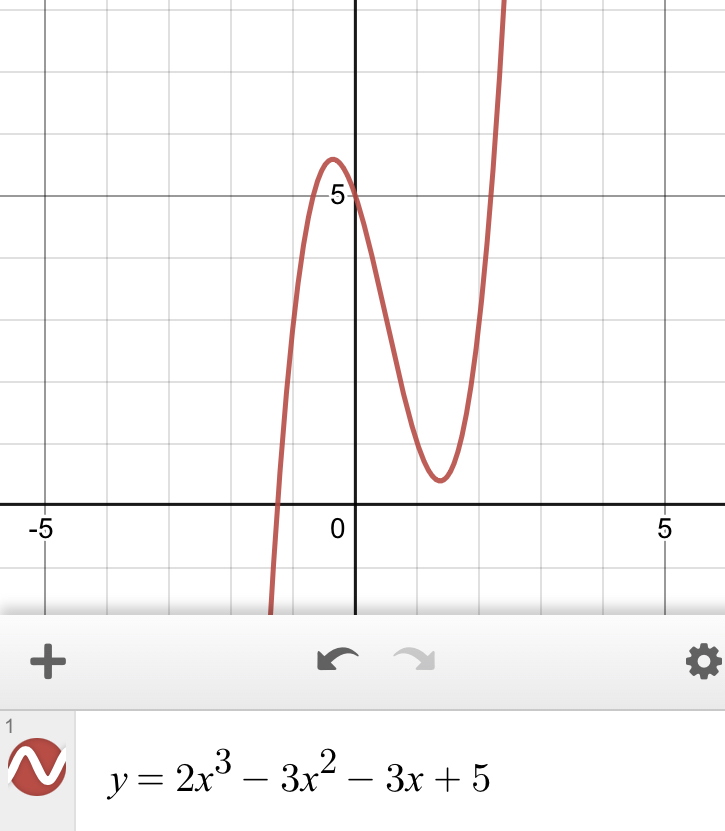
Funciones lineales
El mayor exponente de la variable independiente "x" es 1.
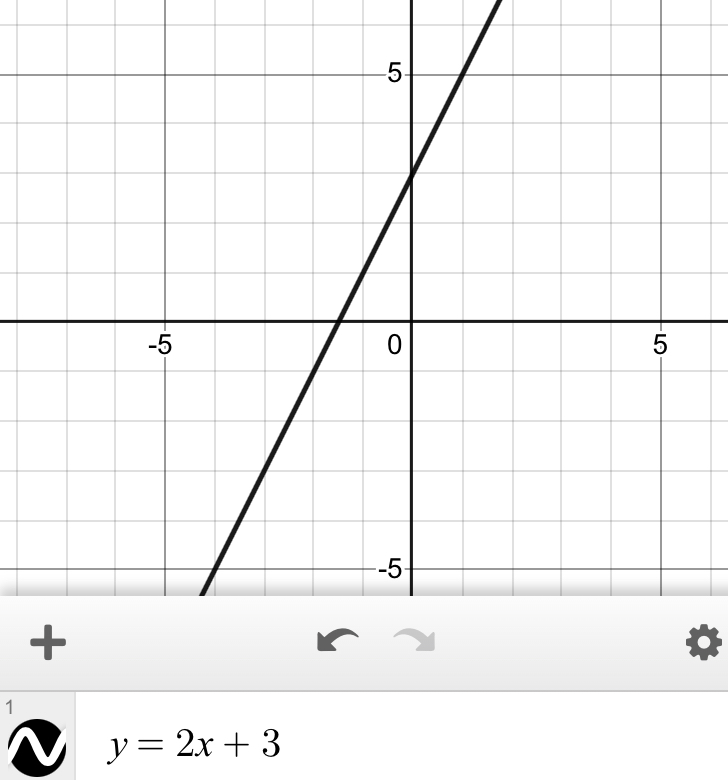
Funciones racionales
Estas funciones se "cortan" o no existen en algunos valores de "x" debido a que en ese valor , el denominador es igual a 0 y al dividir algo entre 0 , la función es indefinida
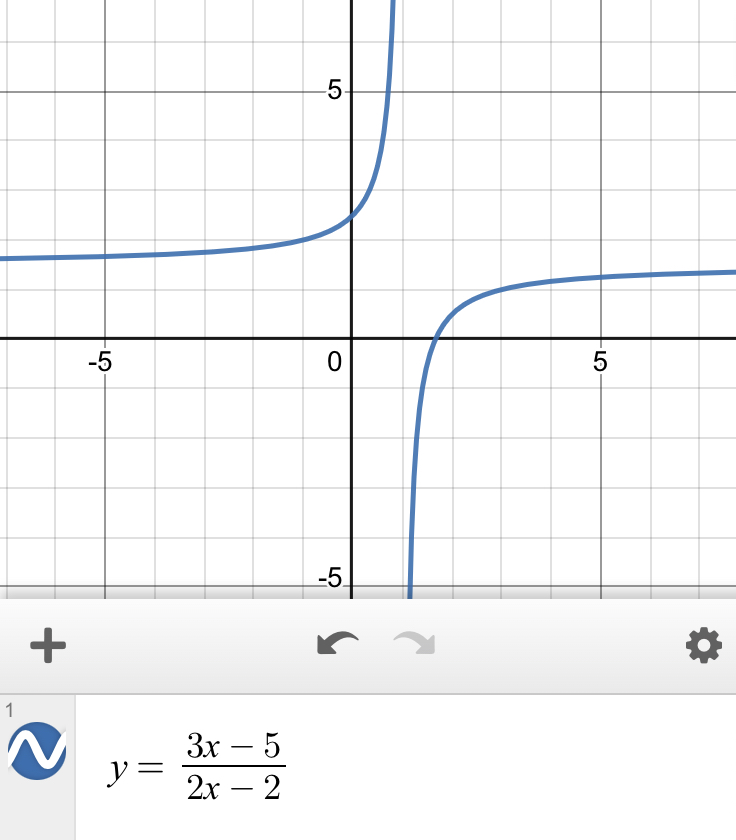
La derivada
Derivada promedio
No nos enfocamos en todos los tipos de funciones y las características de cada una , sino en hablar de manera general para poder comprender las derivadas.
La derivada se define como la razón de cambio o la tasa de cambio entre 2 variables. También se entiende gráficamente como la inclinación o pendiente de una recta. Se denota con la letra "m":
m = 🔺y / 🔺x
donde 🔺 significa cambio (incremento o decremento) y para determinarlo se hace lo siguiente:
m = (y2 - y1) / (x2 - x1)
donde una función pasa por 2 puntos (x1 , y1) y (x2 , y2)
Observamos que en el NUMERADOR se determina el cambio de la variable DEPENDIENTE y en el DENOMINADOR el cambio de la variable INDEPENDIENTE
Función de posición - Su derivada es una función velocidad
Supongamos que la siguiente función describe una persona que se traslada en un patín eléctrico avanzando "y" metros en relación con el tiempo "x" en segundos:
y = 2x2 + 3x
Para obtener la DERIVADA PROMEDIO necesitamos 2 puntos, uno inicial y uno final.
Por ejemplo:
x1 = 2 segundos (s) (tiempo inicial)
y1 = 2(2)2 + 3(2) = 14 metros (m) (posición inicial)
x2 = 8 segundos (s) (tiempo final)
y2 = 2(8)2 + 3(8) = 152 metros (m) (posición final)
La derivada promedio es
m = (152 - 14)m / (8 - 2) s m = 138 m / 6 s m = 23 m / s
CON ESTO , DETERMINAMOS QUE LA DERIVADA DE UNA FUNCIÓN POSICIÓN, ES IGUAL A LA VELOCIDAD (METROS POR SEGUNDO)
Al ser una función cuadrática (parábola) la que describe la posición del patín , en ese intervalo de tiempo (de 2 a 8 segundos) la velocidad va cambiando en cada segundo. Por lo que el resultado de 23 m / s significa que esa es la velocidad promedio a la que se mueve la persona en ese intervalo. Es decir , si calculamos velocidades en distintos segundos dentro del intervalo , todas estarán alrededor de 23 m / s
Derivada instantánea
Para calcular la derivada promedio , se necesita tener 2 puntos (inicial y final). Sin embargo, también podemos encontrar la derivada de una función en un punto específico, lo cual, es la inclinación (pendiente) de la recta tangente a la curva en ese punto. A continuación se muestra un ejemplo en el que se encuentra la recta tangente a la curva cuando x = 0 segundos
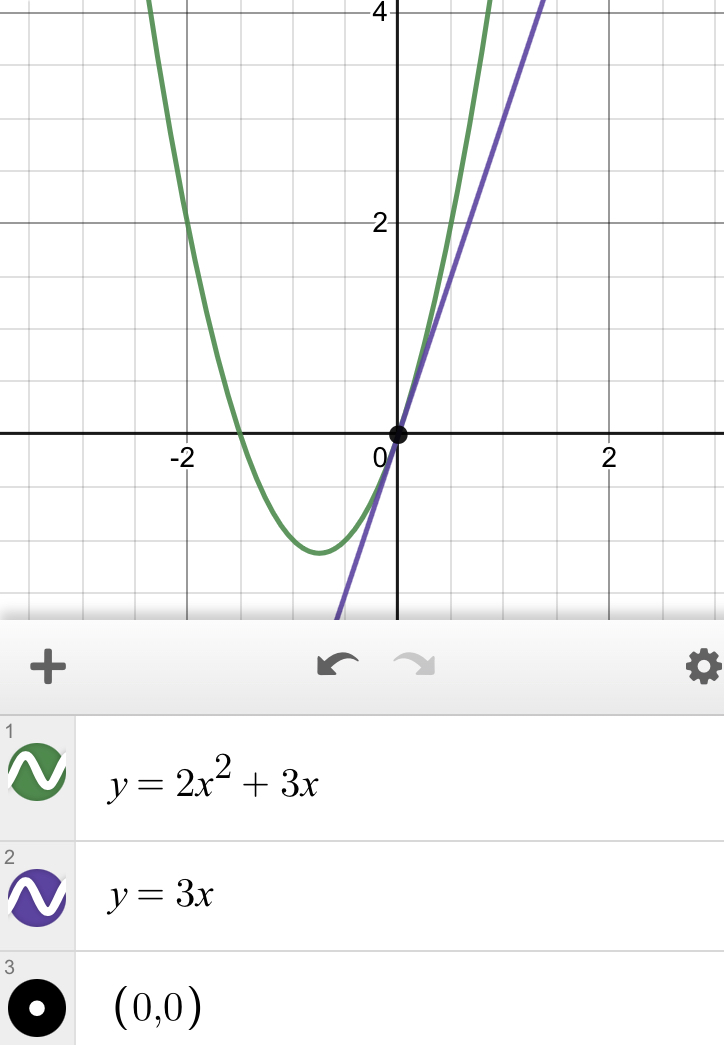
Para derivar una función , aplicaremos la fórmula:
Fórmula para derivar
La función y = xn
donde n es un exponente
La derivada es y' = n xn-1
Ejemplo:
y = x4 , siguiendo la fórmula, n = 4, entonces
y' = 4x4-1 = 4x3
La derivada de la funcion "y" se denota de las siguientes maneras:
dy/dx (derivada de "y" respecto a la variable "x") donde llamamos a dy diferencial de "y"
y' (y prima)
f'(x) (f prima de x : derivada de la función respecto a la variable x)
Volviendo a la función que describe la posición del patín respecto al tiempo y = 2x2 + 3x , la derivamos aplicando la fórmula para cada término:
y' = 2 • 2x2-1 + 3 • x1-1
y' = 4x + 3x0
CUALQUIER NÚMERO ELEVADO A 0 ES IGUAL A 1
y' = 4x + 3•1
y' = 4x + 3
Vamos a encontrar su valor en algunos puntos específicos dentro del intervalo con el que trabajamos en la derivada promedio (2 a 8 segundos) denotado por [0,8]. Para esto, sustituimos el valor de x en la derivada de la función.
x = 3 segundos
y' = 4(3) + 3 = 12 + 3 = 15 m / s
x = 5 segundos
y' = 4(5) + 3 = 20 + 3 = 23 m / s
x = 6 segundos
y' = 4(6) + 3 = 24 + 3 = 27 m / s
x = 7 segundos
y' = 4(7) + 3 = 28 + 3 = 31 m / s
Analizando los resultados , todas las velocidades están alrededor de la velocidad promedio que habíamos calculado antes ,
23 m / s en este intervalo.
Función de velocidad - Su derivada es una función de aceleración
La derivada es el cambio de una variable respecto al cambio de otra. Por definición , la aceleración es el cambio de velocidad respecto al tiempo.
Por último, se muestra una descripción gráfica detallada de la derivada.





